Tips 1: Hur man hittar rätt sexkantssida
Tips 1: Hur man hittar rätt sexkantssida
Sexkantig - "hexagonal" form har,till exempel delar av nötter och pennor, honungskläder och snöflingor. Regelbundna geometriska former sådana former har någon funktion som skiljer dem från andra platta polygoner. den består av att radien av den cirkel runt hexagon lika med längden av dess sidor - i många fall i hög grad förenklar beräkningen av polygon parametrar.

instruktion
1
Om, under förhållandena för problemet, beskrivs radieen (R) nära rätten hexagon Det finns inget att beräkna - detta värde är identiskt med sexkantens sida (t): t = R. För en känd dimmer (D), dela den helt enkelt i halva: t = D / 2.
2
Omkretsen (P) av rätten hexagon tillåter oss att beräkna längden på sidan (t) med en enkel delningsoperation. Använd som divisor antal sidor, dvs. sex: t = P / 6.
3
Radien (r) inskriven i en sådan polygonomkrets är ansluten med sin långsida (t) lite mer komplex koefficient - dubbel radie, och dividera resultatet med kvadratroten av trippel: t = 2 * r / √3. Samma formel med diametern (d) av den inskrivna cirkeln blir en mer matematisk åtgärd: t = d / √3. Till exempel, med en radie av 50 cm, sidolängden hexagon bör vara ungefär lika med 2 * 50 / √3≈ 57,735 cm.
4
Polygonens kända område (S) med sexvertices tillåter oss också att beräkna längden på sidan (t), men den numeriska koefficient som förbinder dem uttrycks exakt i form av en bråkdel av tre naturliga nummer. Dela två tredjedelar av torget av trippelkvoten och från det erhållna värdet extrahera kvadratroten: t = √ (2 * S / (3 * √3)). Till exempel om området av figuren är 400 cm ^, bör dess sidolängd vara approximativt √ (2 * 400 / (3 * √3)) ≈ √ (800/5196) ≈ √153,965 ≈ 12,408 cm.
5
Omkretsen (L) omkrets om höger hexagon, är relaterad till radie och därmed till sidlängden(t) i termer av talet Pi. Om det ges under villkoren för problemet, dela dess värde med två tal Pi: t = L / (2 * π). Om till exempel, om detta värde är 400 cm, bör sidlängden vara ungefär 400 / (2 * 3,142) = 400 / 6,284 ≈ 63,654 cm.
6
Samma parameter (l) för den inskrivna cirkeln gör det möjligt att beräkna längden på sidan hexagon (t) genom att beräkna förhållandet mellan det och produkten av talet Pi av kvadratroten av trippeln: t = l / (π * √3). Till exempel, om längden på den inskrivna cirkeln är 300 cm, sidan hexagon bör ha ett värde ungefär lika med 300 / (3,142 * √3) ≈ 300 / (3,142 * 1,732) ≈ 300 / 5,442 ≈ 55,127 cm.
Tips 2: Hur hittar du en sexkants yta
Per definition är planimetri korrekten polygon kallas en polygon, där sidorna är lika med varandra och vinklarna är lika. En vanlig hexagon är en vanlig polygon, med ett antal sidor lika med sex. Det finns flera formler för beräkning av området med en vanlig polygon.

instruktion
1
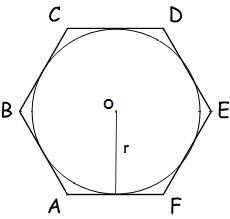
Om radiusen av omkretsen beskrivs närapolygon, kan ytarean beräknas från formeln: S = (n / 2) • R • sin (2π / n), där n - antalet sidor hos polygonen, R - radien för den cirkel, π = 180º.V regelbunden sexhörning alla vinklar är lika 120 °, därför kommer formeln att ha formen: S = √3 * 3/2 * R²

2
I det fall då en cirkel med radie r är inskriven ipolygon, är dess area beräknas genom formeln: S = n * r ^ * tg (π / n), där n - antalet sidor hos polygonen, r - radien av den inskrivna cirkeln, π = 180º.Dlya sexhörning, blir denna formel: S = 2 * √ 3 * r²
3
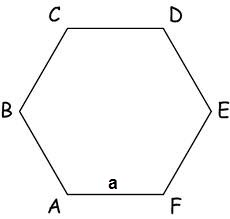
Området med en vanlig polygon kan också varaberäkna, att veta endast längden av dess sidor av formeln: S = n / 4 * a ^ * ctg (π / n), n - antalet sidor hos polygonen, en -, π = 180º.Sootvetstvenno område i sexhörningen är sidolängd av polygonen: S = √3 * 3/2 * a²
Tips 3: Så här hittar du det verkliga tvärsnittet
Egenskaper av figurer i rymden upptas av en sådan geometrisk sektion som stereometri. Den huvudsakliga metoden för att lösa problem i stereometri är metoden avsnitt polyhedra. Det låter dig bygga korrekt avsnitt polyeder och bestämma formen av dessa sektioner.

instruktion
1
Definition av avsnitt vilken som helst figur, det vill säga det naturliga värdet av detta avsnitt, är ofta underförstådd i formuleringen av problem vid konstruktionen av en lutande avsnitt. Den snedställda sektionen är mer korrekt benämnd det främre utskjutande snedplanet. Och för att bygga dess naturliga värde är det tillräckligt att utföra flera åtgärder.
2
Använd en linjal och en penna, rit in en form3 projektioner - framifrån, toppvy och sidovy. På huvudprojektionen, framifrån, visa vägen längs vilken det främre projiceringsplanet passerar, för vilket du drar en lutande linje.
3
Markera huvudpunkterna på den lutande linjen: händelsepunkter avsnitt och avsluta avsnitt. Om formen är en rektangel, så punkternaInträde och utträde kommer att vara en i taget. Om siffran är ett prisma, dubblar antalet poäng. Två punkter definierar inmatning i form och utgång. De andra två bestämmer punkterna på prismans sidor.
4
På ett godtyckligt avstånd rita en rak linje,parallellt med det främre utskjutande sekantplanet. Därefter ritar hjälplinjerna vinkelrätt mot den lutande linjen från punkterna som ligger på huvudvyens axel tills de skär med parallellaxeln. På så sätt får du de projicerade punkterna i figuren i det nya koordinatsystemet.
5
För att bestämma formens bredd, släppa de raka linjerna bortfrån punkterna från huvudvyn till övervyn. Beteckna motsvarande index för projicering av punkterna för varje korsning av linjen och figuren. Till exempel, om punkten A tillhör figurens huvudform, hör punkterna A 'och A till de utskjutande planerna.
6
Sätta åt sidan i det nya koordinatsystemet avståndet,som bildas mellan huvudpunkternas vertikala utsprång. Figuren som erhålls som ett resultat av konstruktion, och är det naturliga värdet hos de lutande avsnitt.