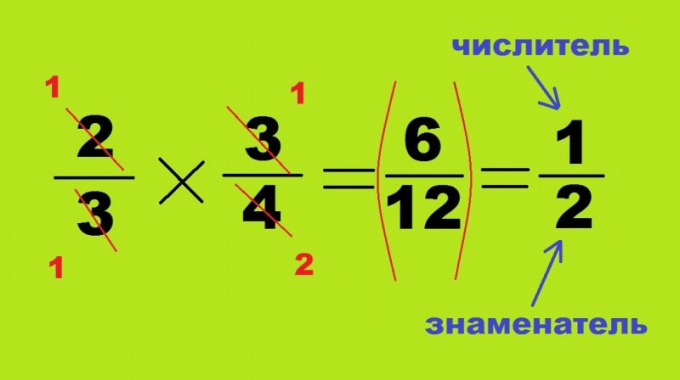LovesTheTeam.com

Du behöver

• Grundkunskaper i matematik.

instruktion

1

Antag att du har två fraktioner: 2/3 och 7/8. Först finner vi den minsta gemensamma delbara nämnaren för dessa fraktioner, och sedan ger vi båda fraktionerna till den. I vårt fall är den minsta gemensamma delbarheten numret 24, så vi kommer att ta med fraktioner till den.

2

För att få den första fraktionen till den hittadesden minsta gemensamma delbara, multiplicera täljaren av den första fraktionen med kvoten att dela denna divisor av täljaren. I vårt fall kommer det att bli: 24/3 = 8. Det vill säga, täljaren av den första fraktionen måste multipliceras med 8. På samma sätt finner vi faktorn för den andra fraktionen: 24/8 = 3. Det vill säga täljaren av den andra fraktionen multipliceras med 3.

3

Vi multiplicerar delarna av fraktionerna med de erhållna partiella fraktionerna. Som ett resultat kommer fraktionerna att ha en gemensam nämnare: 16/24 och 21/24.

Du behöver

• pappersark
• penna eller penna

instruktion

1

Fraktioner med olika täljare och nämnarekan inte jämföras utan deras omvandling. En fraktion kan minskas till någon nämnare, den flera nämnaren för denna fraktion. Det betyder att den nya nämnaren helt måste delas upp i nämnaren av denna fraktion. Till exempel kan den nya nämnaren av 3/8 fraktionen vara nämnaren 32, eftersom 32 är dividerad med 8.

2

Dela den nya nämnaren i den gamla. 32: 8 = 4. Du har en ytterligare multiplikator.

3

För att få fraktionen till en ny nämnare,multiplicera dess täljare och multiplikatorn med ytterligare en faktor. Om du till exempel vill kasta en 3/8 fraktion till nämnaren 32, multiplicera både 3 och 8 med 4.

4

Ge nu de fraktioner som du behöverjämföra med den gemensamma nämnaren. För att jämföra två fraktioner, ta produkten av deras nämnare till den gemensamma nämnaren, eftersom detta tal kommer att vara ett flertal av båda nämnarna. Ett sådant nummer kallas den minsta gemensamma nämnaren. Låt oss säga att du måste jämföra fraktioner 5/7 och 3/5. Först multiplicera nämnarna. När vi multiplicerar 7 med 5 får vi 35. Detta är den gemensamma nämnaren.

5

En ytterligare faktor för fraktionen 5/7 är numret 5, sedan 35: 7 = 5. Multiplicera täljaren och nämnaren av fraktionen med 5. Vi får 25/35.

6

En ytterligare faktor för fraktionen 3/5 är numret 7, sedan 35: 5 = 7. Multiplicera täljaren och nämnaren av fraktionen med 7. Vi får 21/35.

7

Jämför nu de resulterande fraktionerna. Den större (mindre) är den fraktion vars täljare är större (mindre). 25/35> 21/35. Därför 5/7> 3/5. Problemet löser sig framgångsrikt.

Du behöver

• - en bit papper;
• - penna eller penna
• - kalkylator.

instruktion

1

Skriv ett exempel. Antag att du måste lägga till fraktionerna 2 / a och 5 / b. I stället för bokstäver kan det finnas några nummer. Titta på vad som står i täljaren och nämnaren för varje fraktion och huruvida en av dem eller båda kan klippas. Det är lämpligt att göra detta under alla omständigheter, oavsett om samma nämnare härrör från denna åtgärd eller ej. Om du till exempel behöver lägga till 1/3 och 4/6 måste du minska den andra fraktionen. Kom ihåg regeln om sammandragning. Täljaren och nämnaren måste delas in i ett och samma nummer. I ovanstående exempel divideras de med 2. Det visar sig att 4/6 = 2/3, det vill säga 1/3, är det nödvändigt att lägga till 2/3. Resultatet är en.

2

Om fraktionerna inte krymper eller som ett resultatOlika beteckningar erhålls, det är nödvändigt att hitta en gemensam nämnare. Kom ihåg egenskapen av en bråkdel, enligt vilken dess värde inte ändras om de övre och nedre delarna multipliceras med samma nummer. Detta nummer kallas ytterligare en faktor. Hitta det för bråk 2 / a och 5 / b. I detta fall är det nödvändigt att multiplicera nämnarna, det vill säga den ytterligare faktorn kommer att vara lika med en * b.

3

Beräkna, vid vilket nummer det är nödvändigt att multipliceravar och en av fraktionerna för att erhålla samma nämnare. För den första fraktionen blir detta numret b, för det andra - numret a. Således kan varje fraktion representeras i formen 2 / a = 2b / ab; 5 / b = 5a / ab. I det här fallet kan du redan hitta summan eller skillnaden i fraktioner. Summan m = 2b / ab + 5a / ab = (2b + 5a) / ab. På exakt samma sätt finns det en gemensam nämnare för tre eller flera fraktioner.

4

För att göra det lättare med beräkningar leder bråk normalt tillden minsta gemensamma nämnaren. Den är lika med den minsta gemensamma multipeln av de siffror som står i nämnarna av alla data under villkoren för det fraktionerade problemet. Kom ihåg hur den minst gemensamma multipeln beräknas. Det är det minsta numret som är delbart med alla originalnummer. För att göra detta, sönderdela varje nummer till primära faktorer. För att beräkna den minst gemensamma multipeln, multiplicera dem. Varje enkel multiplikator måste tas så många gånger som det förekommer i det nummer där det är störst. Om du till exempel behöver hitta den minsta gemensamma multipeln av nummer 10, 16 och 26, sönderdelas dem enligt följande. 10 = 2 * 5, 16 = 2 * 2 * 2 * 2, 26 = 2 * 13. LOC = 5 * 2 * 2 * 2 * 2 * 13 = 1040. Ur det här exemplet är det uppenbart att en enkel multiplikator 2 måste tas så många gånger som numret 16 sönderdelas.