Tips 1: Så här bestämmer du typen av triangeln
Tips 1: Så här bestämmer du typen av triangeln
En triangel är det enklaste av polygoner. Den består av tre punkter som ligger i ett plan, men inte en rak linje, parvis kopplad av segment. Trianglar kan emellertid vara helt olika och har följaktligen olika egenskaper.
instruktion
1
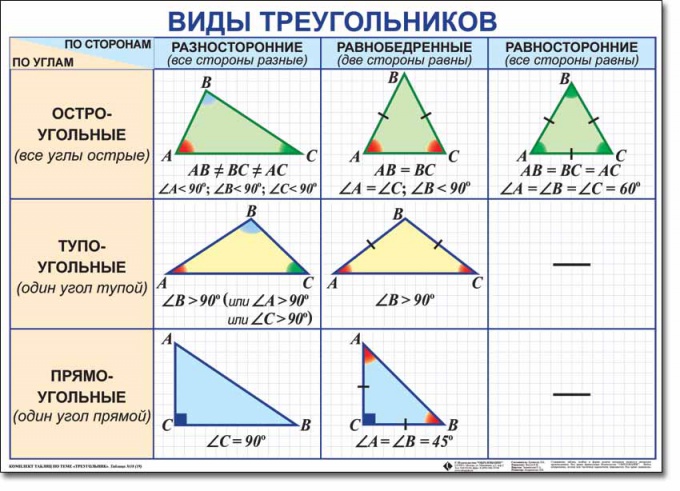
Det är vanligt att utesluta sex arter trianglar. I hjärtat av denna uppdelning finns två klassificeringar: i hörnen och på sidorna. Klassificering av vinklar förutsätter att trianglarna delas in i akut, rektangulär och stump. Klassificering av förhållandet mellan sidor delar trianglarna i mångsidiga, jämnsidiga och isosceles. Och varje triangel hör samtidigt till två slag. Det kan till exempel vara rektangulärt och mångsidigt samtidigt.
2
Definiera formuläret triangel Var vänlig försiktig med typ av hörn. En stump triangel kommer att kallas, där en av hörnen är trubbig, det vill säga mer än 90 grader. En rektangulär triangel kan beräknas genom närvaron av en direkt (lika med 90 grader) vinkel. För att klassificera triangeln lika akut måste du dock se till att alla tre vinklarna är skarpa.
3
Definiera formuläret triangel av förhållandet mellan sidorna, först måste dulära längden på alla tre sidor. Om dock längden på sidorna du inte får, kan vinklar hjälpa dig. Mångsidig kommer att vara en triangel, vars tre sidor har olika längder. Om sidornas längder är okända, kan triangeln klassificeras som mångsidig om alla tre vinklarna är olika. Den mångsidiga triangeln kan vara stump, rektangulär och akut.
4
En likvärdig triangel, två av demvars tre sidor är lika med varandra. Om längden på sidorna inte ges till dig, vägledas av två lika vinklar. Den isosceles triangeln, som den mångsidiga, kan vara både otydlig och rektangulär och akutvinklad.
5
Ekvivalent kan bara namngesEn triangel, vars tre sidor är lika långa. Samtliga vinklar är lika med varandra, och var och en är lika med 60 grader. Därför är det uppenbart att liksidiga trianglar alltid är akuta vinklar.
Tips 2: Hur identifierar du en obtus och akutvinklad triangel
Den enklaste av polygoner är en triangel. Den bildas med hjälp av tre punkter som ligger i ett plan, men inte ligger på en rak linje, parvis förbunden med segment. Trang är dock av olika slag och har därför olika egenskaper.

instruktion
1
Det är vanligt att skilja mellan tre typer av trianglar: stump, akut och rektangulär. Detta är en klassificering efter vinkeltyp. En stump triangel är en där en av vinklarna är trubbiga. Blunt är vinkeln, som är större än nittio grader, men mindre än ett hundra och åttio. Till exempel i vinkeln ABC är vinkeln ABC 65 °, vinkeln BCA är 95 °, vinkeln CAB är 20 °. Vinklarna ABC och CAB är mindre än 90 °, men vinkeln BCA är större, så triangeln är obrukbar.
2
En akut triangel är en triangel varsalla vinklar är skarpa. En vinkel vinkel är en vinkel mindre än nittio och större än noll grader. Till exempel, i triangeln ABC är vinkeln ABC 60 °, vinkeln BCA är 70 °, vinkeln CAB är 50 °. Alla tre vinklarna är mindre än 90 °, så triangeln är akutvinklad. Om du vet att alla sidor av triangeln är lika, betyder det att alla vinklar av det också är lika med varandra, medan de är lika med sextio grader. Följaktligen är alla vinklar i en sådan triangel mindre än nittio grader, och sålunda är en sådan triangel akutvinklad.
3
Om i vinkeln är en av vinklarna lika med nittio grader betyder det att den inte gäller vinkelformen eller den akutvinklade typen. Detta är en rätvinklig triangel.
4
Om triangeln är bestämd av förhållandetpartier, de kommer att vara liksidiga, mångsidiga och likställda. alla parter i en liksidig triangel är lika, och det är hur du fick reda tyder på att akut-vinklad triangel. Om en triangel är lika med endast två parter eller sidor inte är lika, kan det vara trubbig och rektangulära och akut-vinklad. Följaktligen är det i dessa fall nödvändigt att beräkna eller mäta vinklar och göra slutledningar, i enlighet med punkterna 1, 2 eller 3.
Tips 3: Vilka trianglar heter lika
Likvärdigheten av två eller flera trianglar motsvarar fallet när alla sidor och vinklar av dessa trianglar är lika. Det finns dock ett antal enklare kriterier för att bevisa denna jämlikhet.

Du behöver
- Textbok om geometri, ett pappersark, en enkel penna, protractor, linjal.
instruktion
1
Öppna den seventh-grade geometriska läroboken påstycke om tecken på jämlikhet av trianglar. Du kommer att se att det finns ett antal grundläggande funktioner som bevisar likheten mellan två trianglar. Om två trianglar vars jämlikhet är verifierade är godtyckliga, då finns det tre grundläggande tecken på jämlikhet. Om ytterligare information om trianglar är känd kompletteras de tre viktigaste egenskaperna med flera. Detta gäller till exempel fallet med likvärdiga rätvinkliga trianglar.
2
Läs den första regeln om jämlikhettrianglar. Som du vet kan du överväga trianglar lika om du kan bevisa att ett hörn och två intilliggande sidor av två trianglar är lika. För att förstå hur denna lag fungerar, rita på pappersarket med en grader två identiska definierade vinklar bildade av två strålar som kommer från en punkt. Mäta linjalen med samma sidor från toppen av det dragna hörnet i båda fallen. Mät vinklarna på de två formade trianglarna med en grader, se till att de är lika.
3
För att inte tillgripa sådan praktiskåtgärder för att förstå triangeln jämställdhet, läsa bevis på det första tecknet på jämlikhet. Faktum är att varje regeln om lika trianglar har en rigorös teoretisk bevis, det är inte bara användbar för att memorera regler.
4
Läs det andra tecknet på trianglarnas jämlikhet. Det står att två trianglar kommer att vara lika om någon sida och två intilliggande vinklar av två sådana trianglar är lika. För att komma ihåg denna regel, föreställ dig den drabbade sidan av triangeln och två intilliggande hörn. Föreställ dig att längden på sidorna av hörnen gradvis ökar. I slutet kommer de att korsa och bilda en tredje vinkel. I denna mentala uppgift är det viktigt att skärningspunkten för sidorna som ökar mentalt, liksom den resulterande vinkeln, bestäms unikt av tredje part och av två intilliggande hörn.
5
Om du inte har någon information om hörnanvänd sedan det tredje tecknet på jämlikhet av trianglar. Enligt denna regel anses två trianglar vara lika om alla tre sidor av en av dem är lika med motsvarande tre sidor av den andra. Således säger denna regel att längderna på sidorna av en triangel bestämmer helt alla vinklar av en triangel och därmed bestämmer de unikt av triangeln själv.







