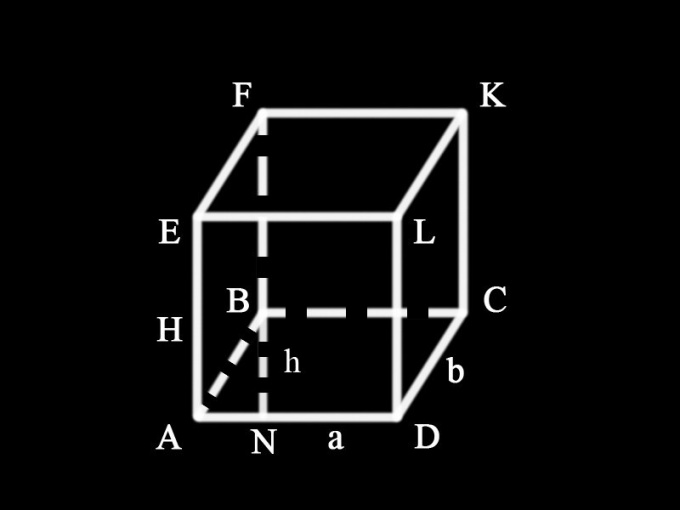
Tips 1: Hur man hittar höjden på ett fyrkantigt prisma
Tips 1: Hur man hittar höjden på ett fyrkantigt prisma
Ett prisma är en volymbild som består avett antal rektangulära sidoytor och två baser parallella med varandra. Baserna kan ha formen av en polygon, inklusive en fyrkant. Höjden på denna figur är segmentet, vinkelrätt mot baserna, mellan planen där de ligger. Dess längd i det allmänna fallet bestäms av lutningsvinkeln hos sidoväggarna mot baserna prisma.

instruktion
1
Om under förhållandena av problemet volymen (V) av utrymmet begränsas av ansikten prisma, och områdets bas (er) för att beräknahöjd (H), använd en formel som är gemensam för prismor med en bas av någon geometrisk form. Dela volymen med basområdet: H = V / s. Till exempel, med en volym av 1200 cm³ och en basarea på 150 cm², höjden prisma bör vara lika med 1200/150 = 8 cm.
2
Om fyrsidan ligger i basen prisma, har formen av någon korrekt siffra, istället för området i beräkningarna kan du använda längderna på kanterna prisma. Till exempel, med en kvadratbas, området iformel i föregående steg, ersätt den andra graden av dess längd (a): H = V / a². Och i fallet med en rektangel i samma formel, ersätt produkten av längden på två angränsande kanter på basen (a och b): H = V / (a * b).
3
Att beräkna höjden (H) hos en vanlig fyrkant prisma Det kan vara tillräckligt att veta det totala områdetyta (S) och längden på ena sidan av basen (a). Eftersom den totala ytan består av områden med två baser och fyra sidoväggar, och i en sådan polyhedron är basen en kvadrat, ytan på en sidoyta måste vara lika med (S-a²) / 4. Detta ansikte har två vanliga kanter med kvadratbaser av känd storlek, för att beräkna längden på den andra kanten, dela det erhållna området vid sidan av torget: (S-a²) / (4 * a). Eftersom prismat i fråga är rektangulärt, ligger kanten av längden beräknad av dig intill baserna i en vinkel av 90 °; sammanfaller med polyhedronens höjd: H = (S-a2) / (4 * a).
4
I rätt fyrkantiga prisma förBeräkning av höjd (H) är tillräcklig för att känna till längden på diagonalen (L) och ena kanten på basen (a). Tänk på triangeln som bildas av denna diagonala, den fyrkantiga diagonalen och en av de laterala revbenen. Kanten här är en okänd kvantitet som sammanfaller med önskad höjd, och kvadratens diagonala, baserat på Pythagoreas teorem, är lika med produkten av sidlängden på de två rotans. I enlighet med samma teori uttrycker du det önskade värdet (katetan) genom diagonalens längd prisma (hypotenus) och basdiagonaler (andra benet): H = √ (L²- (a * V2) ²) = √ (L²-2 * a²).
Tips 2: Hur man gör ett prisma
Ett prisma är en enhet som delar en normalljus på individuella färger: röd, orange, gul, grön, blå, blå, lila. Detta är en transparent objekt med en plan yta som bryter ljusvågor, beroende på deras längd och därmed gör det möjligt att se ljuset i olika färger. göra prisma själv ganska lätt.

Du behöver
- Två pappersark
- folie
- glas
- Kompaktskiva
- Soffbord
- ficklampa
- nål
- vatten
instruktion
1
Prism kan tillverkas av ett enkelt glas. Fyll glaset med vatten lite mer än hälften. Placera glaset på kaffebordets kant så att nästan hälften av glasets botten är upptagen i luften. Se till att glaset är stabilt på bordet.
2
Lägg två pappersark en efter en bredvid soffbordet. Slå på ficklampan och lysa ljuset genom glaset så att det faller på papperet.
3
Justera positionen av facklan och papperet tills du ser en regnbåge på arken - så din ljusstråle lösas i spektra.
Tips 3: Hur man hittar kanten på en fyrkantig pyramid
Den fyrkantiga pyramiden är en pentahedron meden fyrsidig bas och en sidoyta av fyra trekantiga ytor. Polyhedronens sidokanter skär vid en punkt - pyramidens topp.

instruktion
1
En fyrkantig pyramid kan vara korrekt,rektangulär eller godtycklig. En vanlig pyramid har en regelbunden fyrkantig vid basen, och dess apex projiceras till mitten av basen. Avståndet från toppen av pyramiden till basen heter pyramidens höjd. Sidosikten av den vanliga pyramiden är likformiga trianglar, och alla kanter är lika.
2
Vid basen av den vanliga fyrkantiga pyramidenkan ligga kvadratisk eller rektangel. Höjden H för en sådan pyramid projiceras till skärningspunkten mellan basens diagonaler. I kvadraten och rektangeln är diagonalerna d samma. Alla sidokanterna L av pyramiden med en kvadratisk eller rektangulär bas är lika med varandra.
3
För att hitta kanten av pyramiden, övervägaen rätvinklig triangel med sidor: hypotenusan - den erforderliga kanten L, benen - höjden H av pyramiden, och halv av diagonalen d av en bas. Beräkna kanten av Pythagoras sats: kvadraten på hypotenusan är lika med summan av kvadraterna av benen: L ^ = H² + (d / 2) ². I en pyramid med en romb eller en parallellogram i basen motstående kanter är lika och bestäms av formlerna: L₁² = H² + (Di / 2) ² och L₂² = H² + (dj / 2) ², där dj och dj - base diagonal.
4
I den rektangulära fyrkantiga pyramiden av dessVertexen projiceras i en av hörnarnas hörn, planerna på två av de fyra sidoväggarna är vinkelräta mot basens plan. En av kanterna av en sådan pyramid sammanfaller med sin höjd H, och de två sidoväggarna är rektangulära trianglar. Överväga dessa rektangulära trianglar: i vilken en av benen - kanten av pyramiden, som sammanfaller med dess höjd H, de andra benen av - en bas och sidan b, och hypotenusan - okänd pyramid kanter L ^ och L ^. Därför finner du pyramidens två kanter som hypotenusar av rektangulära trianglar: L²² = H² + a² och L²² = H² + b².
5
Den återstående fjärde kanten LNrektangulär pyramid få Pythagoras sats som hypotenusan i en rätvinklig triangel med ben och H d, där d - base diagonal dras från baskanten som sammanfaller med höjden H av pyramiden till bottenkanterna av titel L ^: L₃² = H² + d ^.
6
I en godtycklig pyramid projiceras dess vertex ien slumpmässig punkt på marken. Att hitta kanterna på pyramiden överväga successivt var och en av rektangulära trianglar hypotenusan i vilken - den erforderliga ribba, ett av benen - höjden av pyramiden, och det andra benet - segment som förbinder spetsen med motsvarande bashöjd bas. För att hitta värdena för dessa segment måste överväga trianglarna som bildas i basen vid anslutningspunkten av projektions hörn och en fyrsidig pyramid vinklar.