LovesTheTeam.com

Du behöver

• En lärobok om fysik, ett pappersark, en penna.

instruktion

1

Läs den allmänna definitionen i fysikens läroboktröghetsmomentet för en materialpunkt med avseende på något koordinatsystem eller annan punkt. Såsom är känt bestäms denna kvantitet av produkten av massan av en given materialpunkt vid kvadraten av avståndet från en given punkt, vars tröghetsmoment är bestämt, till koordinatsystemets ursprung eller till den punkt kring vilken tröghetsmomentet bestäms.

2

Observera att i fallet därDet finns flera materialpunkter, tröghetsmomentet i hela systemet av materialpunkter bestäms nästan på samma sätt. För att beräkna tröghetsmomentet hos ett system med materialpunkter i förhållande till ett koordinatsystem är det således nödvändigt att summera alla produkter av massorna av punkterna i systemet med kvadraterna av avstånd från dessa punkter till koordinatsystemets gemensamma ursprung.

3

Observera att i händelse av att istället för en punkt,Om du beräknar tröghetsmomentet, överväga någon axel, så är regeln för beräkning av tröghetsmomentet praktiskt taget oförändrat. Den enda skillnaden är hur avståndet från systemets materialpunkter bestäms.

4

Rita en linje på pappersarket,representerar den aktuella axeln. Bredvid raden på höger och vänster sida, lägg några feta punkter, de kommer att representera materialpunkter. Rita perpendikulär från de angivna punkterna till axellinjen, utan att korsa den. Segmenten du får är faktiskt normala till axelinjen och motsvarar de avstånd som används för att beräkna tröghetsmomentet relativt axeln. Naturligtvis visar din ritning ett tvådimensionellt problem, men i fallet med en tredimensionell situation kommer lösningen att likna om perpendikulär ritas i tredimensionellt utrymme.

5

Kom ihåg från kursen började analysen att närÖvergång från en uppsättning diskreta punkter till en kontinuerlig fördelning av dem, det är nödvändigt att flytta från summering över punkter till integration. Detsamma gäller situationen när du behöver beräkna tröghetsmomentet i förhållande till kroppsaxeln, snarare än ett system med materialpunkter. I detta fall blir summering över poäng integration över hela kroppen med integrationsintervaller bestämda av kroppens gränser. Massan av varje punkt måste representeras som produkten av punktdensiteten med volymdifferensen. Volymdifferensen i sig är uppdelad i en produkt av skillnader i koordinater, längs vilken integration som utförs.

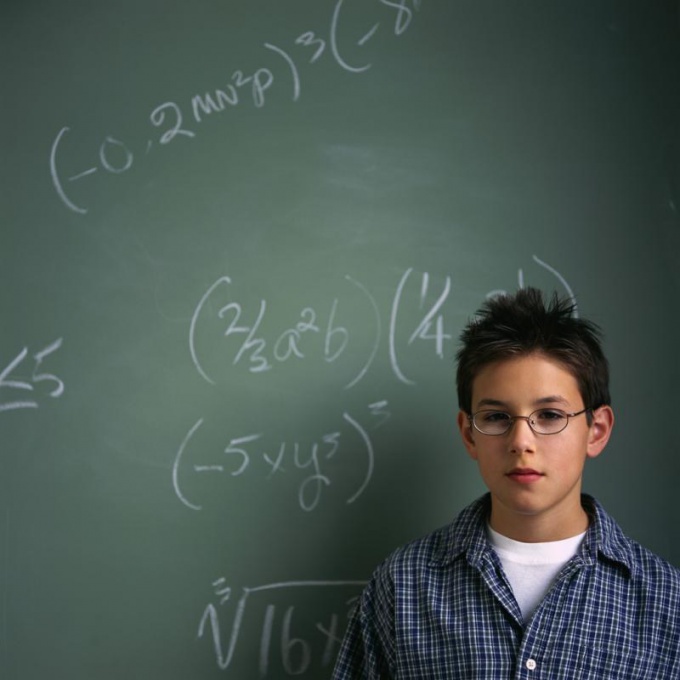
instruktion

1

Tänk på det fysiska uppgift, vilket leder till en differentialekvation, isom inte har argumentet t. Detta är problemet med oscillationer av en matematisk pendul med massa m suspenderad på trådar med längd r i vertikalplanet. Det är nödvändigt att hitta pendulens ekvivalens om det vid det inledande ögonblicket var pendeln stationärt och avvikit från jämviktstillståndet med en vinkel a. Motståndskraften bör försummas (se fig 1a).

2

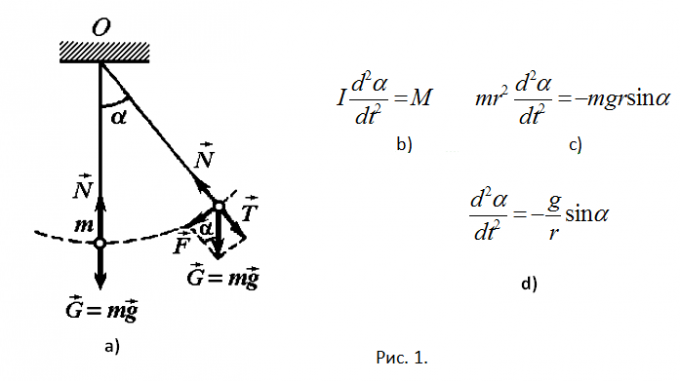
Lösningen. Pendeln är ett material punkt, och suspenderades i en tyngdlös icke töjbara garner vid punkten D. Vid de två krafter: gravitation G = mg och trådspänningskraften N. Båda dessa krafter är i det vertikala planet. Därför, för att lösa problemet kan vara att använda en ekvation i termer av rotationsrörelse kring den horisontella axeln som passerar genom punkten O. Ekvationen av rotationsrörelsen av kroppen har den form som visas i Fig. 1b. I detta fall är jag tröghetsmomentets momentpunkt; j - filamentets vridningsvinkel tillsammans med en punkt, räknat från den vertikala axeln moturs M är momentet av krafter som appliceras på materialpunkten.

3

Beräkna dessa kvantiteter. I = mr ^ 2, M = M (G) + M (N). Men M (N) = 0, eftersom kraftlinjen för kraften passerar genom punkten O. M (G) = - mgrsinj. Tecknet "-" betyder att kraftens ögonblick riktas i motsatt riktning mot rörelsen. Byt tröghetsmomentet och momentet i kraften i rörelsen och få ekvationen som visas i Fig. 1c. Genom att minska massan uppstår ett förhållande (se figur 1d). Det finns inget argument t.

4

I det allmänna fallet är nth-differentialens ekvationför att inte ha x och lösa med avseende på det högsta derivatet y ^ (n) = f (y, y ', y ", ..., y ^ (n-1)). För den andra ordningen är detta y '' = f (y, y '). Lös det genom att ersätta y '= z = z (y). Eftersom för en komplex funktion dz / dx = (dz / dy) (dy / dx), då är y '' = z'z. Detta leder till första ordningens ekvation z'z = f (y, z). Lös det på något av de sätt du känner till och få z = φ (y, C1). Som ett resultat har vi erhållit dy / dx = φ (y, C1), ∫dy / φ (x, C1) = x + C2. Här är C1 och C2 godtyckliga konstanter.

5

Det specifika beslutet beror på vilken typ avdifferentialekvationen för den första ordningen. Så, om det här är en ekvation med separerbara variabler, så löses den direkt. Om denna ekvation är homogen med avseende på y, gäller för lösningen substitutionen u (y) = z / y. För den linjära ekvationen z = u (y) * v (y).

"Nevskaya" - det här är den mest populära spolen blandsportfiskare. Den har ett attraktivt utseende, och är också mycket lätt att underhålla. Denna spole har ett lågt pris. Trommvikten är 90 g. Den rymmer upp till 100 m fiskelinje med en diameter på 0,7 mm. Med hjälp av en skruv med låsmutter, är slutrundan reglerad. I spolen finns en justerbar vagn. Det kan minska trummans rotationshastighet för att rädda fiskaren från att rasa upp linjen. Stark åtdragning kan dramatiskt minska gjutningsavståndet, det är bäst att bromsa trumman med fingret.

"Kiev" - en spole, som är gjord påaxeln och är utrustad med en automatisk retarderare. Diametern hos lindningen är 100 mm. Trumman kan hålla 100 m fiskelinje med en diameter på 0,6 mm. Spolen har en spärrbroms. Bromsar bör endast användas för att fånga tung sked, och medeltunga och lätta bete gjutning avstånd reduceras.

"Obolon" är en spole tillverkad medroterande trumma med 90 °. För att det ska fungera som en tröghetsspole måste du installera trumman över stången. Diametern hos lindningen är 70 mm och placeras 100 m av fiskelinjen med en diameter av 0,4 mm. För spinnning är det av liten användning, det rekommenderas att använda för botten fiskestänger.