Tips 1: Hur konverterar man tal till binär notering
Tips 1: Hur konverterar man tal till binär notering
Förutom det vanliga decimalsystemet radix, det finns andra system. De vanligaste är binära, oktala, hexadecimala. Dessa system används främst inom datateknik. För att konvertera från ett system nummer radix i den andra finns det enkla operationer. Tänk på hur man översätter antal i binär systemet radix från andra system.

instruktion
1
Att översätta oktal antal i binär systemet Det är nödvändigt att presentera var och en av sina siffror i formulärettriad med binära siffror. Exempelvis sönderdelas oktaltalet 765 i triader enligt följande: 7 = 111, 6 = 110, 5 = 101. Resultatet är ett binärt tal 111110101.
2
Att översätta hexadecimal antal i binär systemet radix Det är nödvändigt att presentera var och en av sina siffror i formulärettetrads med binära siffror. Till exempel är det hexadecimala talet 967 uppdelas i tetrader enligt följande: 9 = 1001 6 = 0110 7 = 0111. Resultatet är ett binärt tal 100.101.100.111.
3
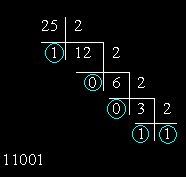
Att konvertera decimaltalet till binärt systemet radix, är det nödvändigt att dela det konsekvent i två, varje gång skriva resultatet som helhet antal och resten. Divisionen måste fortsätt tills ett antal är lika med ett. Det slutliga numret erhålls genom att sekventiellt registrera resultatet av den sista divisionen och remaindersna för alla divisioner i omvänd ordning. Som exempel visar figuren proceduren för att översätta decimal antal 25 till binär systemet radix. Den efterföljande uppdelningen i två ger följande sekvens av rester: 10011. Utvidgning det tvärtom, vi får det erforderliga numret.
Tips 2: Hur konverteras till binärt
Komponenterna i elektroniska maskiner, till vilkadet finns också datorer, det finns bara två urskiljbara tillstånd: det finns en ström och det finns ingen ström. De betecknas "1" respektive "0". Eftersom det bara finns två sådana tillstånd kan många processer och operationer i elektronik beskrivas med binära tal.

instruktion
1
För att översätta en bråkdel av decimalnummer i binärt talsystem, följ följande algoritm. Tänk på algoritmens funktion med exempel på nummer 235.62. Först översätts talets heltalsdel.
2
Dela decimalnumret med två tillsvi får en odelbar rest. Vid varje delningssteg får vi återstoden 1 (om utdelningsnumret är udda) eller 0 (om utdelningen är delbar med två utan återstoden). Alla dessa rester måste beaktas. Sista kvot som erhålls som ett resultat av en sådan uppdelning steg kommer alltid edinitsey.Zapisyvaem sista enheten i MSB hos det binära talet av titel och återstod erhållits under skrivning av denna enhet i omvänd ordning. Här måste du vara försiktig och inte hoppa över nollor. Så kommer numret 235 i binärkoden att motsvara numret 11101011.

3
Översätt nu till binärt talningssystemden delade delen av decimaltalet. För att göra detta multiplicerar vi den delade delen av numret med 2 och fixar heltalets delar av de erhållna numren. Dessa heltal delas till det nummer som erhölls i föregående steg efter binärpunkten i den direkta ordningen. Då motsvarar decimalfrakten 235,62 den binära fraktionen 11101011.100111.

Tips 3: Hur översätter du nummersystemet
I informationstekniken används i stället för det vanliga decimalsystemet, binärt ofta, eftersom datorns arbete är byggt på det.

instruktion
1
Huvudoperationerna är bara två: översättning från decimal till annan (binär, oktal, etc.) och vice versa. Namnet på varje nummersystem kommer från dess bas - antalet element i det (binärt - 2, decimal - 10). I basnotationssystem med en bas som är större än 10 är det vanligt att använda bokstäverna i det latinska alfabetet (A-10, B-11, etc.) som ersättning för tvåsiffriga tal.
2
Låt oss överväga operationerna med hjälp av ett binärt systemnumrering, som den vanligaste. För alla andra system gäller samma regler och metoder för ersättning av bas 2 med motsvarande. Så vi har ett visst nummer i det binära nummersystemet, bestående av flera siffror. Vi skriver det i form av summan av produkterna i sina siffror multiplicerat med 2. Därefter ordnar vi alla krafter från höger till vänster från 0. Vi sammanfattar. Det resulterande numret är det du söker. Exempel. 1011 = 2 * 2 + 11.
3
Överväga nu omvänd operation.Låt det få ett tal i decimal systemet. Vi delar upp det med en kolumn på grundval av nummersystemet som vi vill översätta det (i vårt fall kommer det att bli 2). Divisionen fortsätter i slutet, tills den privata blir mindre än marken. Därefter skriver vi alla rester i raden från och med sista. Detta är det önskade numret. Exempel 11/2 = 5 resten är 1, 5/2 = 2, resten är 1, 2/2 = 1 resten är 0 => 1011. Ett annat exempel visas på bilden. För andra baser är operationerna liknande. Glöm inte att byta ut siffrorna, börjar med 10 i motsvarande antal system i latinska bokstäver! Annars kommer det resulterande numret att läsas felaktigt, eftersom "10" och "1" "0" är helt olika saker! Basen av nummersystemet, där numret representeras, indikeras i form av ett index längst ner till den högsta siffran av numret.

Tips 4: Hur man översätter tal från ett system till ett annat
I kontosystemet som vi använder varderadag, tio siffror - från noll till nio. Därför kallas det ett decimaltal. Men i tekniska beräkningar, särskilt de som är relaterade till datorer, andra systemet, i synnerhet binär och hexadecimal. Så du måste kunna översätta antal från en systemet numrering i en annan.

Du behöver
- - en bit papper;
- - en penna eller penna
- - kalkylator.
instruktion
1
Det binära systemet är det enklaste. Det finns bara två siffror i det - noll och en. Varje siffra av binär antal, som börjar med slutet, motsvarar kraften hos två. Två till noll grad är lika med en, i de första två, i andra-fyra, i tredje-åtta, och så vidare.
2
Antag att du får ett binärt nummer på 1010110. Enheter i den står på andra, tredje, femte och sjunde från slutet av fältet. Därför är det i decimal systemet lika med 2 ^ 1 + 2 ^ 2 + 2 ^ 4 + 2 ^ 6 = 2 + 4 + 16 + 64 = 86.
3
Det inversa problemet är decimalens översättning antal i det binära systemet. Antag att du har ett antal 57. För att få sin binära post måste du sekventiellt dela detta nummer med 2 och skriva resten av divisionen. Det första steget ger dig den sista siffran: 57/2 = 28 (balans 1). Sedan får du den andra från slutet: 28/2 = 14 (resten 0). Nästa steg är: 14/2 = 7 (återstoden 0) 7/2 = 3 (rest 1) 3/2 = 1 (rest 1) 1/2 = 0 (rest 1) .Detta sista steget, eftersom resultatet av divisionen är noll. Som ett resultat, fick du binärt tal 111001.Proverte rätta svaret: 111001 = 2 ^ 0 + 2 ^ 3 + 2 ^ 4 + 2 ^ 5 = 1 + 8 + 16 + 32 = 57.
4
Det andra nummersystemet som används idatorproblem - hexadecimal. Det är inte tio, men sexton siffror. För att inte skapa nya symboler, de första tio siffrorna i hexadecimal systemet betecknas med vanliga siffror, och de återstående sex - i latinska bokstäverna: A, B, C, D, E, F. antalm från 10 till 15. För att undvika förvirring föregås en # eller 0x karaktär av ett tal skrivet på ett hexadecimalt system.
5
Att konvertera ett tal från hexadecimal systemet i decimal måste du multiplicera var och en av dess nummer medmotsvarande grad av sexton och lägg till resultaten. Till exempel är talet # 11A i decimaltallet 10 * (16 ^ 0) + 1 * (16 ^ 1) + 1 * (16 ^ 2) = 10 + 16 + 256 = 282.
6
Omvänd översättning från decimal systemet i hexadecimal görs med samma metodrester, som i binär. Till exempel, ta ett antal 10000. Därefter divideras med 16 och registreringsrester, får du: 10000/16 = 625 (resten 0) 0,625 / 16 = 39 (rest 1) 0,39 / 16 = 2 (rest 7) 0,2 / 16 = 0 (rest 2) resultaten av beräkningarna blir ett hexadecimalt tal # 2710.Proverte rätta svaret: # 2710 = 1 * (16 ^ 1) + 7 * (16 ^ 2) + 2 * (16 ^ 3) = 16 + 1792 + 8192 = 10 tusen.
7
översätta antal från hexadecimal systemet Numreringen i binär är mycket enklare. Numret 16 är en kraft av två: 16 = 2 ^ 4. Därför kan varje hexadecimal siffra skrivas som ett fyrsiffrig binärt tal. Om du har ett binärt tal erhålls mindre än fyra siffror, lägg till toppen av nuli.Naprimer, # 1F7E = (0001) (1111) (0111) (1110) = 1111101111110.Proverte Rätt svar: Båda antal i decimaltallet är 8062.
8
För den omvända översättningen måste du dela upp binärenantalet grupper om fyra siffror, som börjar från änden, och varje sådan grupp ersatt hexadecimala tsifroy.Naprimer, 11000110101001 omvandlas till (0011) (0001) (1010) (1001), vilket i hexadecimal notation ger # 31A9. Svarets korrekthet bekräftas av en översättning i decimalbeteckningen: båda antal är lika med 12713.
Tips 5: Hur konverterar man ett nummer till binärt
På grund av den begränsade användningen av symboler är det binära systemet mest lämpligt för användning i datorer och andra digitala enheter. Symbolerna är bara två: 1 och 0, så här systemet tillämpas i registret.

instruktion
1
Det binära systemet är positionellt,dvs. Positionen för varje siffra i numret motsvarar en viss siffra, vilket är lika med två i motsvarande grad. Graden börjar från noll och ökar när du flyttar från höger till vänster. Till exempel, antal 101 är lika med 1 * 2 ^ 0 + 0 * 2 ^ 1 + 1 * 2 ^ 2 = 5.
2
Att översätta antal från något annat numreringssystem till binärt,du kan använda två metoder: sekventiell uppdelning med 2 eller genom att översätta varje siffra av ett tal i ett bord i motsvarande fyrdubblar av binära tal.
3
En bred fördelning mellan positionssystemAnvänd också oktala, hexadecimala och decimalsystem. Och om för de första två den andra metoden är mer tillämplig, då är båda tillämpliga för översättning från decimalsystemet.
4
Tänk på omvandlingen av ett decimaltal till ett binärt tal systemet genom en metod för successiv uppdelning med 2. För att översätta decimal antal 25 i binär kod måste du dela den med 2 tillså länge det inte förblir 0. Resterna som erhålls vid varje delningssteg skrivs till raden från höger till vänster, efter att ha skrivit siffran i den sista resten, blir detta det sista binära antal. Så: 25/2 = 12, 1 i resten => 1; 12/2 = 6, resten är inte närvarande => 0; 6/2 = 3, resten är inte närvarande => 0; 3/2 = 1, 1 i återstoden => 1; = 0, 1 i återstoden => 1. Översättningen av översättningen är följande: 25_10 = 11001_2.
5
Okal och hexadecimala talöversätts till binär kod genom att ersätta varje siffra motsvarar fyra kodsymbolerna i det binära systemet. Översättningstabellen är som följer: 0 = 0000 1 = 0001, 2 = 0010 3 = 0011, 4 = 0100 5 = 0101 6 = 0110 7 = 0111 8 = 1000 9 = 1001, A = 1010, B = 1011, C = 1100, D = 1101, E = 1110, F = 1111.Naprimer: 61_8 => [6 = 0110] [1 = 0001] => 01100001_2; 9EF_16 => [9 = 1001] [E = 1110] [F = 1111] => 100111101111_2.
Tips 6: Vad är antalet system
Nummersystemet är ett sätt att skriva siffror närhjälp specialtecken, det vill säga representation av numret skriftligt. Nummersystemet ger numret en viss standardrepresentation. Beroende på tid och tillämpningsområde fanns det och fortsätter att finnas många nummer system.

instruktion
1
De befintliga nummersystemen kan delas in i tre huvudtyper: positionell, blandad och icke-positionell.
2
I positioneringssystem, tecknet eller numretkan ha ett annat värde beroende på positionen. Systemet bestäms av antalet symboler som används i den. Det mest populära och mest använda decimalsystemet. I det representeras alla tal av en bestämd sekvens av tio siffror från 0 till 9.
3
Arbetet med all digital teknik bygger på ett binärt talningssystem. Den använder endast två tecken: 1 och 0. Alla stora tal representeras av olika kombinationer av dessa nummer.
4
I vissa beräkningar, den ternära ochoktaltalsystem. Känd är också den så kallade räkningen av dussintals eller det duodecimala nummersystemet. I datavetenskap och programmering är hexadecimal notation mycket populär, eftersom det låter dig skriva ett maskinord - en dataenhet vid programmering.
5
Blandade nummer system liknar positionella. I blandade system representeras siffror av en ökande sekvens. Förhållandet mellan medlemmarna i denna sekvens kan vara helt annorlunda.
6
Så, till det blandade numreringssystemet kan tillskrivasFibonacci-sekvensen, varje tal i vilket är lika med summan av de två föregående numren av sekvensen, börjar med 1. Dvs sekvensen har formen 1, 1 (1 + 0), 2 (1 + 1), 3 (1 + 2), 5 3) och så vidare.
7
Om du representerar en tidsrekord i formatetdygnet-minut-sekund, då är detta också ett blandat antal system. Vilken som helst av termerna i en sekvens kan uttryckas i form av ett minimum, det vill säga på en sekund. Ett ofta använt exempel på ett blandat system i matematik är det faktoriella nummersystemet som representeras av en sekvens av factorials.
8
I icke-position numeriska system, värdetSymbolen för systemet är fast och beror inte på dess position. Dessa system är extremt sällsynta, och de är också matematiskt komplexa. Typiska exempel på sådana system är: Stern-Brocko-nummersystemet, det kvarvarande klasssystemet, binomialtalsystemet.
9
Vid olika tillfällen användes olika folkuppsättning nummersystem. Till exempel var det romerska talsystemet, känt till denna dag, mycket populärt. I det för att skriva siffror användes de latinska bokstäverna V - 5, X - 10, L - 50, C - 100, D - 500, M - 1000.
10
Det fanns också kända sådana nummersystem som singel, quinary, babylonisk, hebreisk, alfabetisk, forntida egyptisk, Maya, Kipu, Inca.







